SAMEN VERJAREN

Bij een groep van enkele tientallen personen, is de kans onverwacht groot dat er twee bij zijn met dezelfde verjaardag.
Bij een gelijkmatige spreiding van de geboortes in de loop van het jaar; is bij 23 personen deze kans 50%, bij 26 personen al 60%.
Ook dit fenomeen hebben we eens bekeken bij de familie Bundervoet-Vermeulen.

Duo's

Beperken we ons tot de generaties van Cyriel en Germaine, de nonkels en de tantes en de neefjes en de nichtjes. Dit betreft een populatie van 55 personen.
De 2 tweelingen Anne-Marie & Marc en Gerda & Greta Verbeke hebben 'van nature uit' dezelfde verjaardag. Hun samenvallende verjaardag wordt daarom niet bij de statistiek in rekening gebracht (wél de samenvallende verjaardag van Gerda & Greta Verbeke samen met die van Marc De Beir!).
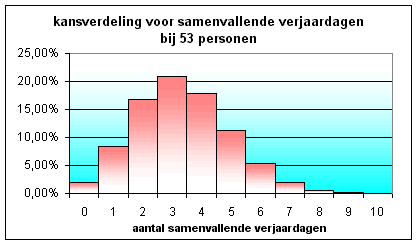
De statistische verdeling van de samenvallende verjaardagen bij 53 personen ziet eruit als hiernaast weergegeven: de kans dat er geen samenvallende verjaardag is, is vrij klein, amper 1,89%. De kansen dat er 1, 2 of 3 samenvallende verjaardagen zijn, stijgen respectievelijk naar 8,30%, 16,86% en 20,98%. Van dan af dalen de kansen terug vrij snel: 17,94%, 11,21%, 5,30% en 1,95% waarbij resp. 4, 5, 6 en 7 duo's samen verjaren (°).

Lieve en Stijn op 26 januari,
Bert en Mieke Verbeke op 26 maart,
Gerda & Greta Verbeke samen met Marc De Beir op 30 maart,
Charles Lebon en Gilbert Van Der Straeten op 15 augustus,
Chris en Wim Verbeke op 20 november.

De familie Bundervoet telt op 53 geboortedagen niet minder dan 5 samenvallende verjaardagen. Zie hiernaast.
Dit is enigszins boven de verwachte waarde, maar evenwel statistisch niet abnormaal, en (héél) ten dele te verklaren door de niet-uniforme spreiding van de geboortes over het jaar.
In het lijstje treffen we verder één Bundervoet-Bundervoetcombinatie (20%), 2 combinaties Bundervoet-niet-Bundervoet (40%) en 2 niet-Bundervoet-niet-Bundervoetcombinaties (40%) aan. Bij een samenstelling van 21 Bundervoeten en 32 niet-Bundervoeten op een totale populatie van 53, sluiten deze percentages vrij goed aan bij de statistisch verwachte waarden van resp. 15,24%, 48,77% en 35,99%.
Dat de (4) kinderen Verbeke met hun 3 verjaardagen (op 3!) tot deze samenvallende geboortedagen behoren is een pure toevalligheid van de natuur, een typische merkwaardigheid bij een 'statistiek achteraf' ...

Dat anderzijds in het gezin Bundervoet-Vermeulen met zijn 14 gekende geboortedagen geen gemeenschappelijke verjaardagen gevierd konden worden is niet min of meer dan normaal. De kans hiertoe is vooralsnog erg klein: slechts 3,56%.

Trio's?

De waarschijnlijkheid voor het vòòrkomen van drie samenvallende verjaardagen werd eveneens berekend. Deze is tamelijk gering: de kans dat géén trio voorkomt bij een populatieomvang van 53 geboortedagen is niet minder dan 85,15%. De kans dat één trio voorkomt is amper 13,38%, voor twee 0,89% en voor drie 0,03%.
We zijn dan ook niet verbaasd dat we, naast het 'pseudo-trio' gevormd door de tweelingzussen Verbeke met Marc De Beir (cfr. supra), geen samenvallende verjaardagen voor drie personen aantreffen in de familie Bundervoet-Vermeulen.

-------------------------------------------------------------------------------------------------------------------------------
(°): Ere wie ere toekomt, voor het opstellen van de formule voor de statistische verdeling van de samenvallende verjaardagen konden we beroep doen op de bereidwillige medewerking van meestercijferaar Bruno ("mooi oefeningske").

Voor wie eraan geïnteresseerd is,
de probabiliteit waarbij n paren een zelfde verjaardag hebben, doch onderling verschillend voor elk paar, wordt uitgedrukt door

P(np*,N,J) = (1/n!) * (N!/(N-2n)!) * (1/2n) * (J!/(J+n-N)!) * (1/JN).

Hierbij is N de populatieomvang (c.q. 53) en J het aantal dagen van het jaar.
Om de zaak niet tot in den treure te compliceren werd J op 365 dagen ingesteld en werd bijgevolg geen rekening gehouden met het vóórkomen van schrikkeljaren en de mogelijkheid om ééns om de vier jaar op 29 februari (samen) te verjaren. Het verlies aan precisie is verwaarloosbaar.